Learning the Ising Model

Introduction

The review of [1-3] aims to implement the training process of the restricted Boltzmann machine on shallow networks to learn the probability distribution of thermal spin configurations associated with the 2D Ising model, which Hamiltonian is given by

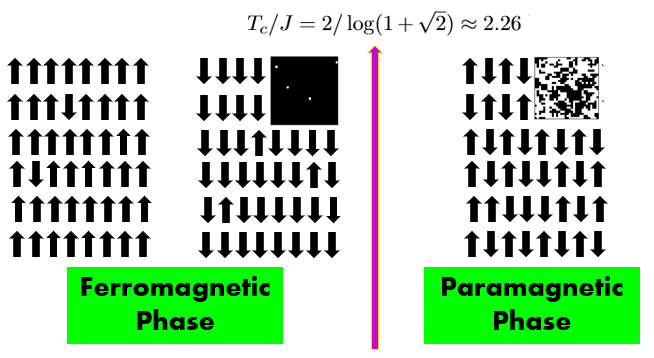
where σi represents the magnetic dipole moment of atomic spins which can be in one of two states (+1 or -1), J is the exchange energy strength and  <i,j> denotes sum over nearest neighbors on a square lattice with periodic boundary conditions. The system develops a phase transition at the critical temperature Tc/J = 2.26 between two different phases of matter i) a high temperature T>Tc -> paramagnetic phase (PM) and ii) a low temperature T<Tc -> ferromagnetic phase (FM)

 

Dataset

Monte Carlo simulations were performed to generate spin configuration samples for the 2D Ising model around the critical temperature Tc. The samples are weighted by the Boltzmann distribution following detailed balance and ergodicity as fundamental principles. 

The size of the square lattice is N=LxL, where we choose L= 4,30,50 to simulate enough data to sample physical observables and train the different neural networks presented throughout the post. In all study cases, the data is divided in three sets a) training 70%, b) validation 20%, and c) testing 10%. The data set consists of a large matrix of size RxL^2, where the columns/features store the dipole moments of the spins distributed on the square lattice, while the rows/observations represents different spin configurations.

The number of observations for the different study cases are:

·       RBM.- 50000 observations at each temperature T/J in [1,3.5] with steps of Delta T = 0.1, on a lattice size of L=4.

·       Unsupervised learning. - 250 observations at each temperature T/J in [1,3.5] with steps of Delta T = 0.1, on a lattice size of L=30.

·       Supervised learning. - 100 observations at each temperature T/J in [1,3.5] with steps of Delta T = 0.1, on a lattice size of L=50.

 Study Cases

 I.- Restricted Boltzmann machine

The RBM is trained to learn the probability distribution corresponding to spin configurations on a lattice of size L=4 at a given temperature T. 

The RBM is an Energy Based Model defined by 

 

which consists of one visible layer (V1,V2,..,Vm), one hidden layer (h1, h2,..,hn), biases bi, cj and weights Wij, where no two neurons within the same layer connected. The model parameters = W,b,c are trained on thermal spin configurations to learn the probability distribution of the Ising model, and then efficiently sample new spin configurations. The training of the RBM consists of 2 steps i) Given a vector V , which in our case are the spin configurations, we use the conditional probability p(h|V) to make a prediction of h (Forward Pass). Then, given h the conditional probability p(V|h) is used to make a prediction of V (Backward Pass), and so on. ii) The update of the model parameters= W,b,c takes place after minimizing the Kullback-Leibler divergence between the target probability distribution and the model probability distribution observed on the visible layer. Finally, steps i) and ii) are repeated until desired accuracy is achieved.

 

The below figure shows measurements of the heat capacity per Ising spin on samples obtained from Monte Carlo simulations and by the trained RBM. The number of hidden neurons encodes a lower dimensional representation of the spin probability distribution and thus is the most important hyperparameter to be tuned as Ref. [2] points out.

II.- Supervised Learning

The phases of the 2D Ising model are classified by a supervised learning approach on a data set corresponding to a lattice size of L=30. The labels represent whether a spin configuration was generated with T<Tc (label 0 corresponding to FM phase) or T>Tc (label 1 corresponding to PM phase). The architecture of the neural network consists of a feed forward fully connected NN with an input layer of N=L^2 neurons (corresponding to the magnetic dipole moment of Ising spins), a single hidden layer containing 100 neurons and an output layer with two neurons. Sigmoid activation functions are used within the hidden and output layers. The cost function selected correspond to the cross-entropy with L2 regularization and minimized by the Adam optimizer. 

 

The below picture shows a) the average of the output layer and b) accuracy over the test sets vs. temperature. Note that near the near the critical temperature the NN is not sure if the state corresponds to a PM or FM phase. This interesting behavior can be used to reasonably approximate the critical temperature.

Next figure shows the accuracy and cost function vs trained epoch over the training and test sets.

III.- Unsupervised Learning

 The goal of this section is to use Principal component analysis to generate a lower-dimensional representation of the original high-dimensional dataset corresponding to a lattice size of L=50. For instance, the below figure shows a) a scatter plot of the first two principal components with 3 cluster colored according to their temperature. The central red cluster corresponds to the high-temperature (paramagnetic) phase, whereas the red/blue clusters located to the right/left corresponds to the low-temperature (ferromagnetic) phase (one for the spin-up and the other for the spin-down state), (b-c) are imshow plots for the first two components

It is noteworthy mention that the averages over the set of temperatures of the first two principal components can be used to estimate the critical temperature, see right panel of the below picture, while the left panel shows results from the standard approach of computing the expectation value for physical observables.

Finally, the below picture show a t-SNE  and clustering plots for the lower-dimensional representation of the original data, not surprisingly showing analogous behavior to the PCA scatter plot.

 

 References

[1] Carrasquilla, Juan, and Roger G. Melko. "Machine learning phases of matter." Nature Physics 13.5 (2017): 431-434.

[2] Morningstar, Alan, and Roger G. Melko. "Deep learning the ising model near criticality." The Journal of Machine Learning Research 18.1 (2017): 5975-5991.

[3] Hu, Wenjian, Rajiv RP Singh, and Richard T. Scalettar. "Discovering phases, phase transitions, and crossovers through unsupervised machine learning: A critical examination." Physical Review E 95.6 (2017): 062122.